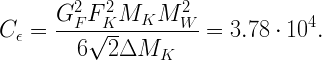Powered by Foswiki, The Free and Open Source Wiki

Difference: ConstraintEpsK (1 vs. 6)

Revision 6

30 Jun 2010 - Main.AdrianBevan

Line: 1 to 1
	Constraint from $\varepsilon_K$
Changed:
< <	Indirect CP violation in the Kaon system is usually expressed in terms of $\| \varepsilon_K \|$ parameter which is the fraction of CP violating component in the mass eigenstates and which is usually defined as:
> >	Indirect CP violation in the Kaon system is usually expressed in terms of $\| \varepsilon_K \|$ parameter which is the fraction of the CP violating component in the mass eigenstates and which is usually defined as:
	$\varepsilon_K = \frac{e^{i\pi/4}}{\sqrt{2}\Delta M_K} \left( \Im{M_{12}}+2\xi\Re{M_{12}} \right ),$
Line: 14 to 14
	Top and charm quarks contribute to the expression of the mixing in K⁰-K⁰ system. The calculation of the box diagram gives
Changed:
< <	M_{12} = \frac{G_F^2}{12\pi^2} F_K^2 B_K M_K M_W^2 \left [ \lambda_c^{2} \eta_t S_0 (x_c) + \lambda_t^{2} \eta_2 S_0 (x_t)+2\lambda_t^* \lambda_c^* \eta_3 S(x_c,~x_t) \right ] with $\lambda_i^=V^_{is}V_{id},$
> >	M_{12} = \frac{G_F^2}{12\pi^2} F_K^2 B_K M_K M_W^2 \left [ \lambda_c^{2} \eta_t S_0 (x_c) + \lambda_t^{2} \eta_2 S_0 (x_t)+2\lambda_t^* \lambda_c^* \eta_3 S(x_c,~x_t) \right ] where $\lambda_i^=V^_{is}V_{id},$
	which allows one to write
Line: 26 to 26
	C_\epsilon = \frac{G_F^2 F_K^2 M_K M_W^2}{6\sqrt{2}\pi^2 \Delta M_K } = 3.84 \cdot 10^4.
Changed:
< <	The expression actually used in the UT fit is obtained writing $\| \varepsilon_K \|$ in terms of $(\bar{\rho},~\bar{\eta})$ and the other elements of CKM matrix:
> >	The expression actually used in the UT fit is obtained by writing $\| \varepsilon_K \|$ in terms of $(\bar{\rho},~\bar{\eta})$ and the other elements of CKM matrix:
	$\| \varepsilon_K \| = C_\epsilon B_K A^2 \lambda^6 \bar{\eta} \left \{ -\eta_1 S_0(x_c) (1-\lambda^2/2) + \eta_3 S_0 (x_c,~x_t) + \eta_2 S_0(x_t) A^2 \lambda^4 (1-\bar{\rho}) \right \}.$
Line: 38 to 38
	Set plot = EpsKRhoEta? -->
Changed:
< <	EPS - PDF - PNG - JPG - GIF
> >	EPS - PDF - PNG - JPG - GIF

Revision 5

09 May 2010 - Main.AdminUser

Line: 1 to 1
	Constraint from $\varepsilon_K$
Line: 34 to 34

Changed:
< <	[EPS format] [JPG format]
> >	<-- Set plot = EpsKRhoEta? --> EPS - PDF - PNG - JPG - GIF

Revision 4

06 Apr 2010 - Main.VittorioLubicz

Line: 1 to 1
	Constraint from $\varepsilon_K$
Line: 14 to 14
	Top and charm quarks contribute to the expression of the mixing in K⁰-K⁰ system. The calculation of the box diagram gives
Changed:
< <	M_{12} = \frac{G_F^2}{12\pi^2} F_K^2 B_K M_K M_W^2 \left [ \lambda_c^{2} \eta_t S_0 (x_c) + \lambda_t^{2} \eta_2 S_0 (x_t)+2\lambda_t^* \lambda_c^* \eta_3 S(x_c,~x_t) \right ] with $\lambda_i^=V^_{is}V_{id},$
> >	M_{12} = \frac{G_F^2}{12\pi^2} F_K^2 B_K M_K M_W^2 \left [ \lambda_c^{2} \eta_t S_0 (x_c) + \lambda_t^{2} \eta_2 S_0 (x_t)+2\lambda_t^* \lambda_c^* \eta_3 S(x_c,~x_t) \right ] with $\lambda_i^=V^_{is}V_{id},$
	which allows one to write
Line: 25 to 23
	where
Changed:
< <	C_\epsilon = \frac{G_F^2 F_K^2 M_K M_W^2}{6\sqrt{2} \Delta M_K } = 3.78 \cdot 10^4.
> >	C_\epsilon = \frac{G_F^2 F_K^2 M_K M_W^2}{6\sqrt{2}\pi^2 \Delta M_K } = 3.84 \cdot 10^4.
	The expression actually used in the UT fit is obtained writing $\| \varepsilon_K \|$ in terms of $(\bar{\rho},~\bar{\eta})$ and the other elements of CKM matrix:
Line: 36 to 34

Changed:
< <	[EPS format] [JPG format]
> >	[EPS format] [JPG format]

Revision 3

04 Apr 2010 - Main.VincenzoVagnoni

Line: 1 to 1

Added:
> >	Constraint from $\varepsilon_K$
	Indirect CP violation in the Kaon system is usually expressed in terms of $\| \varepsilon_K \|$ parameter which is the fraction of CP violating component in the mass eigenstates and which is usually defined as: $\varepsilon_K = \frac{e^{i\pi/4}}{\sqrt{2}\Delta M_K} \left( \Im{M_{12}}+2\xi\Re{M_{12}} \right ),$

Revision 2

02 Apr 2010 - Main.VincenzoVagnoni

Line: 1 to 1
Changed:
< <	-- VincenzoVagnoni - 01 Apr 2010
> >	Indirect CP violation in the Kaon system is usually expressed in terms of $\| \varepsilon_K \|$ parameter which is the fraction of CP violating component in the mass eigenstates and which is usually defined as: $\varepsilon_K = \frac{e^{i\pi/4}}{\sqrt{2}\Delta M_K} \left( \Im{M_{12}}+2\xi\Re{M_{12}} \right ),$ where $\xi=\frac{\Im{A_{\pi\pi.~I=0}}}{\Re{A_{\pi\pi.~I=0}}}.$ Top and charm quarks contribute to the expression of the mixing in K⁰-K⁰ system. The calculation of the box diagram gives $M_{12} = \frac{G_F^2}{12\pi^2} F_K^2 B_K M_K M_W^2 \left [ \lambda_c^{2} \eta_t S_0 (x_c) + \lambda_t^{2} \eta_2 S_0 (x_t)+2\lambda_t^* \lambda_c^* \eta_3 S(x_c,~x_t) \right ]$ with $\lambda_i^=V^_{is}V_{id},$ which allows one to write $\varepsilon_K=C_\epsilon B_K A^2 \Im{\lambda_t} \left \{ \Re{\lambda_c} \left [ \eta_1 S_0(x_c) - \eta_3 S_0 (x_c,~x_t) A^2 \lambda^4 \right ] - \Re{\lambda_t} \eta_2 S_0(x_t) \right \} e^{i \pi /4},$ where $C_\epsilon = \frac{G_F^2 F_K^2 M_K M_W^2}{6\sqrt{2} \Delta M_K } = 3.78 \cdot 10^4.$ The expression actually used in the UT fit is obtained writing $\| \varepsilon_K \|$ in terms of $(\bar{\rho},~\bar{\eta})$ and the other elements of CKM matrix: $\| \varepsilon_K \| = C_\epsilon B_K A^2 \lambda^6 \bar{\eta} \left \{ -\eta_1 S_0(x_c) (1-\lambda^2/2) + \eta_3 S_0 (x_c,~x_t) + \eta_2 S_0(x_t) A^2 \lambda^4 (1-\bar{\rho}) \right \}.$ The experimental values we use are summarized in the Table of Inputs. The representation of this constraint in the $(\bar{\rho},~\bar{\eta})$ plane is given below. [EPS format] [JPG format]

View topic | History: r6 < r5 < r4 < r3 | More topic actions...

Ideas, requests, problems regarding this web site? Send feedback

Difference: ConstraintEpsK (1 vs. 6)

Constraint from

Constraint from

Constraint from

Constraint from

Constraint from
$\varepsilon_K$

Constraint from
$\varepsilon_K$

Constraint from
$\varepsilon_K$

Constraint from
$\varepsilon_K$