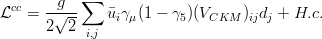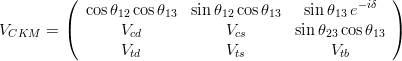Under construction
The Cabibbo-Kobayashi-Maskawa ( CKM) matrix
V_{CKM}=\left(\begin{array}{ccc} V_{ud} & V_{us} & V_{ub}\\ V_{cd} & V_{cs} & V_{cb}\\ V_{td} & V_{ts} & V_{tb}\end{array}\right)
is a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the SU(2)_L quark doublet of the Standard Model ( SM). In the mass eigenstate basis, the CKM matrix appears in the SM charged current interaction
{\cal L}^{cc}=\frac{g}{2\sqrt{2}} \sum_{i,j} \bar u_i \gamma_\mu (1-\gamma_5) (V_{CKM})_{ij} d_j+ H.c.
The CKM matrix elements are the only flavour- and CP-violating couplings present in the SM.
The CKM matrix can be parametrized using three rotation angles .\theta_{12},\theta_{13},\theta_{22} in [0,\pi/2] and one phase \delta in (-\pi,\pi]. The standard parametrization reads
V_{CKM}=\left(\begin{array}{ccc} \cos\theta_{12}\cos\theta_{13}& \sin\theta_{12}\cos\theta_{13}& \sin\theta_{13}\, e^{-i\delta}\\ V_{cd} & V_{cs} & \sin\theta_{23}\cos\theta_{13}\\ V_{td} & V_{ts} & V_{tb}\end{array}\right)
We extract the CKM parameters from the measurements of \vert V_{ud}\vert,\,\vert V_{cb}\vert,\,\vert V_{ub}\vert and \gamma using
\begin{array}{ll}\sin\theta_{13}=\vert V_{ub}\vert, & \cos\theta_{13}=\sqrt{1-\sin^2\theta_{13}},\\ \cos\theta_{12}=\frac{\vert V_{ud}\vert}{\cos\theta_{13}}, & \sin\theta_{12}=\sqrt{1-\cos^2\theta_{12}},\\ \sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}.
The sign + (-) in the formula for \delta corresponds to \cos\gamma<0~(\cos\gamma>0).
 
  Powered by
Foswiki Ideas, requests, problems regarding this web site? Send feedback