- Home
- Constraints
- Fit Results
- Historical Plots
- Papers and Conferences
- CKM Formalism
- Statistical Method
- Contacts
- Feedback
Gamma Combination from the UTfit goup
We use the relevant post-Moriond 2012 HFAG averages as inputs.
The results of combination:
| Parameter | Full fit |
|---|---|
![\gamma [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_d441395f3c6b5d6d14b98a13ae4b8837.png) |
 |
![\delta_{B}(DK) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_41e661b01cefdd9ec2084738b64160f3.png) |
 |
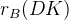 |
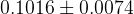 |
![\delta_{B}(DK^{*}) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_1baa48393b03b96f22571066583a25b8.png) |
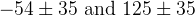 |
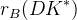 |
 |
![\delta_{B}(D^{*}K) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_5211b61dcb830d9a98ee9a7878d74aff.png) |
 |
 |
 |
|
|
|
|
|
|
|
The angle  of the CKM triangle can be measured comparing
of the CKM triangle can be measured comparing  and
and  mediated transitions in
mediated transitions in  decays. The decays proceed through the following diagrams:
decays. The decays proceed through the following diagrams:

These diagrams are practically free from the New Physics contribution.
There are three methods to extract relevant information, each of them deals with its own  decay:
decay:
 and the relative
and the relative  conserving phase
conserving phase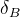 between the two amplitudes. These parameters depend on the
between the two amplitudes. These parameters depend on the  decay under investigation.
decay under investigation.
 of the CKM triangle can be measured comparing
of the CKM triangle can be measured comparing  and
and  mediated transitions in
mediated transitions in  decays. The decays proceed through the following diagrams:
decays. The decays proceed through the following diagrams:

 decay:
decay:
- a singly Cabibbo-suppressed CP eigenstate, like
 for Gronau-London-Wyler (GLW) method;
for Gronau-London-Wyler (GLW) method;
- a doubly Cabibbo-suppressed flavor eigenstate, like
 for Atwood-Dunietz-Soni (ADS) method;
for Atwood-Dunietz-Soni (ADS) method;
- a Cabibbo-allowed self-conjugate 3-body state, like
 for Giri-Grossman-Soffer-Zupan (GGSZ) method.
for Giri-Grossman-Soffer-Zupan (GGSZ) method.
 and the relative
and the relative  conserving phase
conserving phase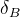 between the two amplitudes. These parameters depend on the
between the two amplitudes. These parameters depend on the  decay under investigation.
decay under investigation.
The Gronau-London-Wyler (GLW) method (M. Gronau, D. Wyler, Phys. Rev. Lett. B {\bf 253} (1991) 483; M. Gronau, D. London, Phys. Rev. Lett. B {\bf 265} (1991) 172) is based on the reconstruction of the  decay to
decay to  , where
, where  and
and  decay
to
decay
to  -even or
-even or  -odd eigenstates. The
-odd eigenstates. The  modes normally used are:
modes normally used are: 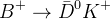 , with
, with  is also reconstructed.
The four observables for this method are formed in the following
way:
is also reconstructed.
The four observables for this method are formed in the following
way:
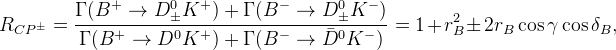
 This set can provide an information on
This set can provide an information on  ,
, 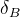 , and
, and  with an 8-fold ambiguity for the phases.
with an 8-fold ambiguity for the phases.
 decay to
decay to  , where
, where  and
and  decay
to
decay
to  -even or
-even or  -odd eigenstates. The
-odd eigenstates. The  modes normally used are:
modes normally used are: -
 :
:  ,
,  ;
;
-
 :
: 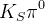 ,
,  ,
, 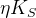 ,
, 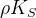 , and
, and 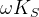 .
.
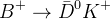 , with
, with  is also reconstructed.
The four observables for this method are formed in the following
way:
is also reconstructed.
The four observables for this method are formed in the following
way:
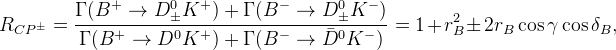
 This set can provide an information on
This set can provide an information on  ,
, 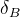 , and
, and  with an 8-fold ambiguity for the phases.
with an 8-fold ambiguity for the phases.
In the ADS method (I. Dunietz, Phys. Rev. Lett. B 270 (1991) 75; Phys. Rev. Lett. D 52 (1995) 3048; D. Atwood, I. Dunietz and A. Soni, Phys. Rev. Lett. 78, 3257 (1997)), 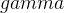 is measured from the study of
is measured from the study of  decays, where
decays, where  mesons decay into non
mesons decay into non  eigenstate final states. The suppression of
eigenstate final states. The suppression of  transition with respect to the
transition with respect to the 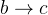 one is partly overcome by the study of decays of the
one is partly overcome by the study of decays of the  meson in final states which can proceed in two ways: either through a favored
meson in final states which can proceed in two ways: either through a favored 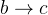
 decay followed by a doubly-Cabibbo-suppressed
decay followed by a doubly-Cabibbo-suppressed  decay, or through a suppressed
decay, or through a suppressed 
 decay followed by a Cabibbo-favored
decay followed by a Cabibbo-favored  decay.
Neglecting
decay.
Neglecting  -mixing effects, which in the SM give very small corrections to \g\ and do not affect the
-mixing effects, which in the SM give very small corrections to \g\ and do not affect the  measurement, the measured ratios
measurement, the measured ratios 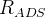 and
and 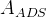 are related to the
are related to the  and
and  mesons' decay parameters through the following relations:
mesons' decay parameters through the following relations:
![R_{ADS}=\frac{\Gamma(B^{+}\rightarrow [\bar f]_{D^{0}} K^{+})+\Gamma(B^{-}\rightarrow [f]_{D^{0}} K^{-})}{\Gamma(B^{+}\to[f]_{D^{0}} K^{+})+\Gamma(B^{-}\to[\bar f]_{D^{0}} K^{-})}=r_{B}^2+r_{D}^2+2 r_{B} r_{D} k_{D}\cos\gamma\cos\delta),](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_3990a6d3e356836f34988a5deee19d2b.png) $%A_{ADS}=\frac{\Gamma(B^{-}\rightarrow [f]_{D^{0}}K^{-})}{\Gamma(\Bp\to [\bar f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
with
\begin{equation}\begin{split}
\rD^2 \equiv\frac{\Gamma(\Dz\to f)}{\Gamma(\Dz\to \bar f)}=
\frac{\int dm\, A_{\rm DCS}(m)}{\int dm\, A_{\rm CA}(m)},\\kD e^{i\deltaD}\equiv \frac{\int dm\, A_{\rm DCS}(m)A_{\rm CA}
e^{i\delta(m)}}{\sqrt{\int dp\, A_{\rm DCS}^2(p)\int dp\, A_{\rm
CA}^2(p)}},
\end{split}\end{equation}
$%A_{ADS}=\frac{\Gamma(B^{-}\rightarrow [f]_{D^{0}}K^{-})}{\Gamma(\Bp\to [\bar f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
with
\begin{equation}\begin{split}
\rD^2 \equiv\frac{\Gamma(\Dz\to f)}{\Gamma(\Dz\to \bar f)}=
\frac{\int dm\, A_{\rm DCS}(m)}{\int dm\, A_{\rm CA}(m)},\\kD e^{i\deltaD}\equiv \frac{\int dm\, A_{\rm DCS}(m)A_{\rm CA}
e^{i\delta(m)}}{\sqrt{\int dp\, A_{\rm DCS}^2(p)\int dp\, A_{\rm
CA}^2(p)}},
\end{split}\end{equation}
![R_{ADS}=\frac{\Gamma(B^{+}\rightarrow [\bar f]_{D^{0}} K^{+})}{\Gamma(B^{+}\to[f]_{D^{0}} K^{+})}=r_{B}^2+r_{D}^2+2 r_{B} r_{D} k_{D}\cos(\gamma+\delta),](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_c7793e0374d42904399c8b8779141f28.png) $%A_{ADS}=\frac{\Gamma(\Bm\to [f]_{\Dz}\Km)}{\Gamma(\Bp\to [\bar
f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
The used observables are connected to the ``classical'' $\rads$ and $\aads$ set by simple relations:
$\rads=\frac{\rplus+\rminus}{2}$ and $\aads=\frac{\rminus-\rplus}{\rminus+\rplus}$.
Since $\rplus$ and $\rminus$ are two independent observables, while
$\rads$ and $\aads$ are correlated we prefer to extract the physical
parameters from $(\rplus,\rminus)$ rather than $(\rads,\aads)$.
The values of \kD\ and \deltaD\ measured by the CLEO-c
collaboration~\cite{cite:CLEO}, are used in the
signal yield estimation and
\rB\ extraction. The ratio \rD\ has been
measured in different experiments and we take the average value~\cite{cite:PDG}.
$%A_{ADS}=\frac{\Gamma(\Bm\to [f]_{\Dz}\Km)}{\Gamma(\Bp\to [\bar
f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
The used observables are connected to the ``classical'' $\rads$ and $\aads$ set by simple relations:
$\rads=\frac{\rplus+\rminus}{2}$ and $\aads=\frac{\rminus-\rplus}{\rminus+\rplus}$.
Since $\rplus$ and $\rminus$ are two independent observables, while
$\rads$ and $\aads$ are correlated we prefer to extract the physical
parameters from $(\rplus,\rminus)$ rather than $(\rads,\aads)$.
The values of \kD\ and \deltaD\ measured by the CLEO-c
collaboration~\cite{cite:CLEO}, are used in the
signal yield estimation and
\rB\ extraction. The ratio \rD\ has been
measured in different experiments and we take the average value~\cite{cite:PDG}.
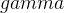 is measured from the study of
is measured from the study of  decays, where
decays, where  mesons decay into non
mesons decay into non  eigenstate final states. The suppression of
eigenstate final states. The suppression of  transition with respect to the
transition with respect to the 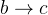 one is partly overcome by the study of decays of the
one is partly overcome by the study of decays of the  meson in final states which can proceed in two ways: either through a favored
meson in final states which can proceed in two ways: either through a favored 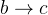
 decay followed by a doubly-Cabibbo-suppressed
decay followed by a doubly-Cabibbo-suppressed  decay, or through a suppressed
decay, or through a suppressed 
 decay followed by a Cabibbo-favored
decay followed by a Cabibbo-favored  decay.
Neglecting
decay.
Neglecting  -mixing effects, which in the SM give very small corrections to \g\ and do not affect the
-mixing effects, which in the SM give very small corrections to \g\ and do not affect the  measurement, the measured ratios
measurement, the measured ratios 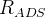 and
and 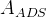 are related to the
are related to the  and
and  mesons' decay parameters through the following relations:
mesons' decay parameters through the following relations:
![R_{ADS}=\frac{\Gamma(B^{+}\rightarrow [\bar f]_{D^{0}} K^{+})+\Gamma(B^{-}\rightarrow [f]_{D^{0}} K^{-})}{\Gamma(B^{+}\to[f]_{D^{0}} K^{+})+\Gamma(B^{-}\to[\bar f]_{D^{0}} K^{-})}=r_{B}^2+r_{D}^2+2 r_{B} r_{D} k_{D}\cos\gamma\cos\delta),](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_3990a6d3e356836f34988a5deee19d2b.png) $%A_{ADS}=\frac{\Gamma(B^{-}\rightarrow [f]_{D^{0}}K^{-})}{\Gamma(\Bp\to [\bar f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
with
\begin{equation}\begin{split}
\rD^2 \equiv\frac{\Gamma(\Dz\to f)}{\Gamma(\Dz\to \bar f)}=
\frac{\int dm\, A_{\rm DCS}(m)}{\int dm\, A_{\rm CA}(m)},\\kD e^{i\deltaD}\equiv \frac{\int dm\, A_{\rm DCS}(m)A_{\rm CA}
e^{i\delta(m)}}{\sqrt{\int dp\, A_{\rm DCS}^2(p)\int dp\, A_{\rm
CA}^2(p)}},
\end{split}\end{equation}
$%A_{ADS}=\frac{\Gamma(B^{-}\rightarrow [f]_{D^{0}}K^{-})}{\Gamma(\Bp\to [\bar f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
with
\begin{equation}\begin{split}
\rD^2 \equiv\frac{\Gamma(\Dz\to f)}{\Gamma(\Dz\to \bar f)}=
\frac{\int dm\, A_{\rm DCS}(m)}{\int dm\, A_{\rm CA}(m)},\\kD e^{i\deltaD}\equiv \frac{\int dm\, A_{\rm DCS}(m)A_{\rm CA}
e^{i\delta(m)}}{\sqrt{\int dp\, A_{\rm DCS}^2(p)\int dp\, A_{\rm
CA}^2(p)}},
\end{split}\end{equation}
![R_{ADS}=\frac{\Gamma(B^{+}\rightarrow [\bar f]_{D^{0}} K^{+})}{\Gamma(B^{+}\to[f]_{D^{0}} K^{+})}=r_{B}^2+r_{D}^2+2 r_{B} r_{D} k_{D}\cos(\gamma+\delta),](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_c7793e0374d42904399c8b8779141f28.png) $%A_{ADS}=\frac{\Gamma(\Bm\to [f]_{\Dz}\Km)}{\Gamma(\Bp\to [\bar
f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
The used observables are connected to the ``classical'' $\rads$ and $\aads$ set by simple relations:
$\rads=\frac{\rplus+\rminus}{2}$ and $\aads=\frac{\rminus-\rplus}{\rminus+\rplus}$.
Since $\rplus$ and $\rminus$ are two independent observables, while
$\rads$ and $\aads$ are correlated we prefer to extract the physical
parameters from $(\rplus,\rminus)$ rather than $(\rads,\aads)$.
The values of \kD\ and \deltaD\ measured by the CLEO-c
collaboration~\cite{cite:CLEO}, are used in the
signal yield estimation and
\rB\ extraction. The ratio \rD\ has been
measured in different experiments and we take the average value~\cite{cite:PDG}.
$%A_{ADS}=\frac{\Gamma(\Bm\to [f]_{\Dz}\Km)}{\Gamma(\Bp\to [\bar
f]_{\Dz}\Kp)}=\rB^2+\rD^2+2\rB\rD\kD\cos(\g-\delta),
The used observables are connected to the ``classical'' $\rads$ and $\aads$ set by simple relations:
$\rads=\frac{\rplus+\rminus}{2}$ and $\aads=\frac{\rminus-\rplus}{\rminus+\rplus}$.
Since $\rplus$ and $\rminus$ are two independent observables, while
$\rads$ and $\aads$ are correlated we prefer to extract the physical
parameters from $(\rplus,\rminus)$ rather than $(\rads,\aads)$.
The values of \kD\ and \deltaD\ measured by the CLEO-c
collaboration~\cite{cite:CLEO}, are used in the
signal yield estimation and
\rB\ extraction. The ratio \rD\ has been
measured in different experiments and we take the average value~\cite{cite:PDG}.
Powered by
 Ideas, requests, problems regarding this web site? Send feedback
Ideas, requests, problems regarding this web site? Send feedback
 Ideas, requests, problems regarding this web site? Send feedback
Ideas, requests, problems regarding this web site? Send feedback

![\,\gamma [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_346b4369d40fd8964bda0f769a5b4bbe.png)

![\,\delta_{B}(DK) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_de1251af0a072fb83f6dd951669769db.png)



![\,\delta_{B}(DK^{*}) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_5164e268a514bb26250f2bad6b8038e2.png)



![\,\delta_{B}(D^{*}K) [^{\circ}]](/foswiki/pub/UTfit/GammaFromTrees/_MathModePlugin_59f1351d3c4dd771bf1d0e886a13457a.png)


