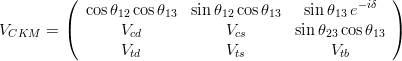Difference: Formalism (1 vs. 14)
Revision 14
20 Sep 2011 - Main.MarcoCiuchini
Revision 13
20 Oct 2010 - Main.MarcoCiuchini
Revision 12
21 Jul 2010 - Main.VincenzoVagnoni
Revision 11
16 Jul 2010 - Main.VincenzoVagnoni
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Changed: | ||||||||
| < < |
Under construction
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the misalignment in flavour space of the up and down components of the | |||||||
| > > |
| |||||||
| -\sin\theta_{12}\cos\theta_{23}-\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{12}\cos\theta_{23}-\sin\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{13}\sin\theta_{23}\ | ||||||||
| Changed: | ||||||||
| < < |
\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,. The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with  , ,  and and  , ,  are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by  . The UT is determined by one complex number . The UT is determined by one complex number namely by the coordinates  in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of  and and  using using
| |||||||
| > > |
\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,.
The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which
    , ,  and and  , ,  are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by  . The UT is determined by one complex number . The UT is determined by one complex number
  in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of  and and  using using
| |||||||
| \cos\theta_{12}=\frac{\vert V_{ud}\vert}{\cos\theta_{13}}, & \sin\theta_{12}=\sqrt{1-\cos^2\theta_{12}},\\sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}. | ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The CKM matrix can be expanded as The exact and expanded relations between the UT apex coordinates  and the Wolfenstein parameters are given by and the Wolfenstein parameters are given by At the lowest order in  , ,  and and  coincide with coincide with  and and  . . | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations
   and the Wolfenstein parameters are given by and the Wolfenstein parameters are given by
  , ,  and and  coincide with coincide with  and and  . . | |||||||
Revision 10
29 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Changed: | ||||||||
| < < |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the misalignment in flavour space of the up and down components of the | |||||||
| > > |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the misalignment in flavour space of the up and down components of the | |||||||
-\sin\theta_{12}\cos\theta_{23}-\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{12}\cos\theta_{23}-\sin\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{13}\sin\theta_{23}\\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,. The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with  , ,  and and  , ,  are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by  . The UT is determined by one complex number . The UT is determined by one complex number namely by the coordinates  in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of  and and  using using
| ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The CKM matrix can be expanded as The exact and expanded relations between  and the Wolfenstein parameters are given by and the Wolfenstein parameters are given by At the lowest order in  , ,  and and  coincide with the UT apex coordinates coincide with the UT apex coordinates  and and  . . | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The CKM matrix can be expanded as The exact and expanded relations between the UT apex coordinates  and the Wolfenstein parameters are given by and the Wolfenstein parameters are given by At the lowest order in  , ,  and and  coincide with coincide with  and and  . . | |||||||
Revision 9
29 Jun 2010 - Main.AdrianBevan
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Changed: | ||||||||
| < < |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
| > > |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the misalignment in flavour space of the up and down components of the | |||||||
-\sin\theta_{12}\cos\theta_{23}-\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{12}\cos\theta_{23}-\sin\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{13}\sin\theta_{23}\\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,. The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with  , ,  and and  , ,  are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by  . The UT is determined by one complex number . The UT is determined by one complex number namely by the coordinates  in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of  and and  using using
| ||||||||
Revision 8
28 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Under construction
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | ||||||||
| Line: 7 to 7 | ||||||||
| \sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}. | ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations At the first order,  is the Cabibbo angle and is the Cabibbo angle and  and and  coincide with the UT coordinates coincide with the UT coordinates  and and  . The exact relation between . The exact relation between 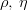 and and  is given by is given by </latex></latex> | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the sine of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The CKM matrix can be expanded as The exact and expanded relations between  and the Wolfenstein parameters are given by and the Wolfenstein parameters are given by At the lowest order in  , ,  and and  coincide with the UT apex coordinates coincide with the UT apex coordinates  and and  . . | |||||||
Revision 7
28 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Changed: | ||||||||
| < < |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
| > > |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
| -\sin\theta_{12}\cos\theta_{23}-\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{12}\cos\theta_{23}-\sin\theta_{12}\sin\theta_{13}\sin\theta_{23}\, e^{i\delta} & \cos\theta_{13}\sin\theta_{23}\ | ||||||||
| Changed: | ||||||||
| < < |
\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,. We start extracting the CKM parameters from the measurements of 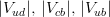 and and 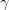 using using
| |||||||
| > > |
\sin\theta_{12}\sin\theta_{23}-\cos\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & -\cos\theta_{12}\sin\theta_{23}-\sin\theta_{12}\sin\theta_{13}\cos\theta_{23}\, e^{i\delta} & \cos\theta_{13}\cos\theta_{23}\end{array}\right)\,. The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with  , ,  and and  , ,  are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by are the non-trivial sides and angles of the normalized UT. The third side is the unit vector and the third angle is given by  . The UT is determined by one complex number . The UT is determined by one complex number namely by the coordinates  in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of in the complex plane of its only non-trivial apex (the others being (0,0) and (1,0)). Several experimental constraints can be conveniently represented on this plane and used to determine the UT, as shown in section Fit Results. We start extracting the CKM parameters from the measurements of  and and  using using
| |||||||
| \cos\theta_{12}=\frac{\vert V_{ud}\vert}{\cos\theta_{13}}, & \sin\theta_{12}=\sqrt{1-\cos^2\theta_{12}},\\sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}. | ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints, discussed in section Constraints, are then applied using the method described in section Statistical Method. Fit Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations At the first order,  is the Cabibbo angle and is the Cabibbo angle and  and and  coincide with the UT coordinates coincide with the UT coordinates  and and  . The exact relation between . The exact relation between 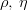 and and  is given by is given by </latex></latex> | |||||||
Revision 6
17 Jun 2010 - Main.AchilleStocchi
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Under construction
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | ||||||||
Revision 5
17 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
Under construction
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | ||||||||
| Line: 7 to 7 | ||||||||
| \sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}. | ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to 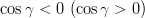 . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to  . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with | |||||||
Revision 4
16 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Changed: | ||||||||
| < < |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
| > > |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
| \cos\theta_{12}=\frac{\vert V_{ud}\vert}{\cos\theta_{13}}, & \sin\theta_{12}=\sqrt{1-\cos^2\theta_{12}},\\sin\theta_{23}=\frac{\vert V_{cb}\vert}{\cos\theta_{13}}, & \cos\theta_{23}=\sqrt{1-\sin^2\theta_{23}},\end{array} ~~\delta=2\arctan\left(\frac{1\mp\sqrt{1-(a^2-1)\tan^2\gamma}}{(a-1)\tan\gamma}\right), ~a=\frac{\cos\theta_{12}\sin\theta_{13}\sin\theta_{23}}{\sin\theta_{12}\cos\theta_{23}}. | ||||||||
| Changed: | ||||||||
| < < |
The sign  in the formula for in the formula for  corresponds to corresponds to 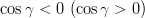 . . | |||||||
| > > |
The sign  in the formula for in the formula for  corresponds to corresponds to 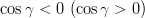 . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle . Additional constraints are then applied using the method described in the section Statistical Method. Results are also given in the popular Wolfenstein parametrization which allows for a transparent expansion of the CKM matrix in terms of the small Cabibbo angle  . The Wolfenstain parameters . The Wolfenstain parameters  are defined by the following equations are defined by the following equations The relations induced by the unitarity of the CKM matrix include six "triangular" relations, among which is referred to as the Unitarity Triangle ( UT). It can be rewritten as with | |||||||
Revision 3
11 Jun 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Changed: | ||||||||
| < < |
| |||||||
| > > |
The Cabibbo-Kobayashi-Maskawa ( CKM) matrixis a 3x3 unitary matrix which originates from the disalignment in flavour space of the up and down components of the | |||||||
Revision 2
18 May 2010 - Main.MarcoCiuchini
| Line: 1 to 1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Under construction | ||||||||
| Added: | ||||||||
| > > |
| |||||||
View topic | History: r14 < r13 < r12 < r11 | More topic actions...
Powered by
 Ideas, requests, problems regarding this web site? Send feedback
Ideas, requests, problems regarding this web site? Send feedback
 Ideas, requests, problems regarding this web site? Send feedback
Ideas, requests, problems regarding this web site? Send feedback
 and
and  , while
, while  is the weak coupling constant and
is the weak coupling constant and  is the field which creates the
is the field which creates the  vector boson. The CKM matrix elements are the only flavour-non-diagonal and CP-violating couplings present in the SM. In general, the CKM matrix can be parametrized using three rotation angles and one phase. The parametrization is however not unique. The standard parametrization, advocated by the PDG, uses
vector boson. The CKM matrix elements are the only flavour-non-diagonal and CP-violating couplings present in the SM. In general, the CKM matrix can be parametrized using three rotation angles and one phase. The parametrization is however not unique. The standard parametrization, advocated by the PDG, uses  in
in ![[0,\pi/2]~](/foswiki/pub/UTfit/Formalism/_MathModePlugin_9727fd85a0a15fa30280bf89f6be2378.png) and
and ![(-\pi,\pi]~](/foswiki/pub/UTfit/Formalism/_MathModePlugin_11d16201edbf57b5634f35a4edd3cafb.png) defined so that
defined so that
 quark doublet of the Standard Model ( SM). In the quark mass eigenstate basis, the CKM matrix appears in the SM charged-current interaction Lagrangian
quark doublet of the Standard Model ( SM). In the quark mass eigenstate basis, the CKM matrix appears in the SM charged-current interaction Lagrangian 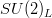 quark doublet of the Standard Model ( SM). In the quark mass eigenstate basis, the CKM matrix appears in the SM charged-current interaction Lagrangian
quark doublet of the Standard Model ( SM). In the quark mass eigenstate basis, the CKM matrix appears in the SM charged-current interaction Lagrangian  and
and 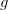 is the weak coupling constant and
is the weak coupling constant and 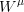 is the field which creates the
is the field which creates the 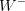 vector boson. The CKM matrix elements are the only flavour- and CP-violating couplings present in the SM. In general, the CKM matrix can be parametrized using three rotation angles and one phase. The parametrization is however not unique. The standard parametrization, advocated by the PDG, uses
vector boson. The CKM matrix elements are the only flavour- and CP-violating couplings present in the SM. In general, the CKM matrix can be parametrized using three rotation angles and one phase. The parametrization is however not unique. The standard parametrization, advocated by the PDG, uses  in
in ![[0,\pi/2]](/foswiki/pub/UTfit/Formalism/_MathModePlugin_73e40ef7b3aa437628df055b85658888.png) and
and ![(-\pi,\pi]](/foswiki/pub/UTfit/Formalism/_MathModePlugin_5274755a90f82e76034c6660a7fee565.png) defined so that
defined so that 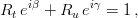
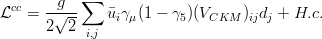
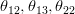 in
in